Understanding aerodynamic forces is essential to designing vehicles such as aircraft and cars. A designer’s goal is generally to maximize “aerodynamic “efficiency” in order to improve fuel economy. This is a tedious task, considering that aerodynamic forces are functions of numerous flow and geometric parameters. In this article, we will try to understand the basic aerodynamic forces and their easier-to-understand representations, or “Aerodynamic Coefficients.”.
Aerodynamic Coefficients and Flow Parameters
As stated earlier, aerodynamic force is not only dependent on the geometric properties of the body but also on fluid properties such as density, viscosity, temperature and pressure. Moreover, relative flow speed and angle play a more dominant role in force generation. The angle of attack (Alpha or AOA) is the relative angle of fluid velocity and the mean line or cord line of the airfoil. This flow angle plays a dominating role in the generation of aerodynamic forces. The choice of the axis system is also important in order to understand the effect of these forces.

The wind axis (three-dimensional) and stability axis (two-dimensional) are the two important axis systems to represent the aerodynamic forces. Both axis systems have their x-axis aligned to the direction of the flow (transformation/resolved by AOA); this choice is kind of intuitional as the forces represented in the stability axis are either normal (lift) or opposite to the direction of flight.

Dimension Reduction
If all factors effecting the aerodynamic forces are to be considered, then the equation of force may look like this:

As stated above, many combinations of these parameters will generate the same flow field and resultant forces. But equations can be resolved by dimensional analysis, resultant relationship will be simplified in terms of reduced parameters.

These reduced parameters are very intuitive; for example, dynamic pressure is a measure of the kinetic energy of the flow; speed of sound or Mach number, is essentially the measure of the traveling pressure wave in the fluid. The Reynolds number is a ratio of flow momentum to viscous forces.
Non-dimensional Aerodynamic Coefficients
One further step to further simplify the aerodynamic forces is to represent them in terms of non-dimensional coefficients, so that the effect of scale will be eliminated. For example, flow around a Formula-1 car and its wind tunnel model are essential, but the scale of forces being generated is quite different. This approach helps in comparative analysis as well, as comparison of the aerodynamic configurations will be simple, provided forces are normalized by a common dimension (such as cord length or surface area). Hence, the equations of lift and drag coefficient are as follows:

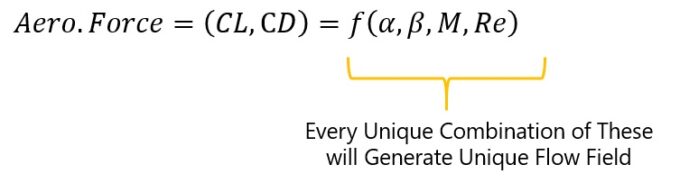
In their final form, the dependency of the aerodynamic coefficients is quite simple; we only have flow angles Alpha (AOA) and Beta (Angle of Sideslip), Mach numbers, and Reynolds number. Only unique combinations of these parameters will suffice for aerodynamic analysis or wind-tunnel testing.
Origin of Aerodynamic Forces
Aerodynamic forces are generated due to the interaction of the body’s surface with fluid; obviously, they originate at the surface of the body. Pressure in the fluid (also called “static pressure”) acts normal to the surface boundary. The interaction of the fluid in a tangential direction is a little more complex, but strictly speaking, the fluid exerts a wall shear stress at the surface of the body. The net pressure force is computed by the integral (summation) of the pressure across the surface of the body.
Similarly, total shear force is computed by the summation of the shear stress across the surface of the body. The present discussion is about free-stream flow, and there is another region around the body where the shear effects are dominant; this region is called the “Boundary Layer”. (Read this article about boundary layer: https://www.engineersvault.com/aerospace/a-look-into-the-boundary-layer/ )



